import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import networkx as nx
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.nn.init as init
from torch_geometric.datasets import Planetoid
import torch.optim as optim
import matplotlib.animation as animation
from IPython.display import HTML
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
from sklearn.manifold import TSNEIn this post I am implementing Graph Convolutional Layer
Basic Imports
Importing Planetoid dataset - Cora
dataset = Planetoid(root='data/Planetoid', name='Cora')def visualize(h, color):
# Perform t-SNE dimensionality reduction
z = TSNE(n_components=2).fit_transform(h.detach().cpu().numpy())
# Create a scatter plot of the t-SNE embeddings
plt.figure(figsize=(10, 10))
plt.xticks([])
plt.yticks([])
plt.scatter(z[:, 0], z[:, 1], s=70, c=color, cmap="Set2")
plt.show()Visulization of the dataset
visualize(dataset[0].x, dataset[0].y)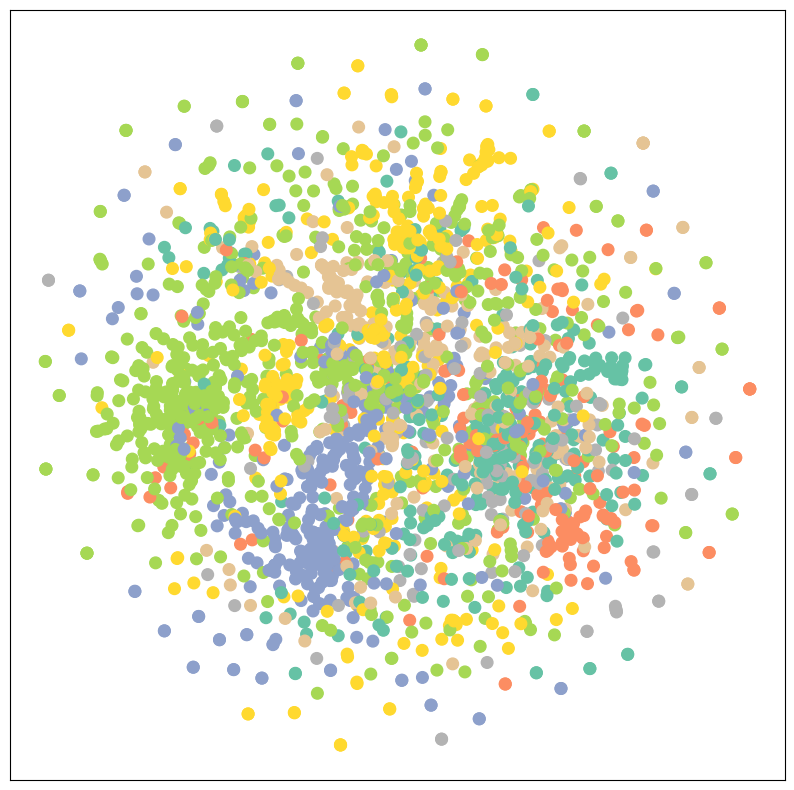
# convert pytorch tensor to networkx graph
def to_networkx(data):
G = nx.Graph()
G.add_nodes_from(range(data.num_nodes))
G.add_edges_from(data.edge_index.t().tolist())
return GG = to_networkx(dataset[0])Creating the Adjacency Matrix
# Adjacency matrix
A = nx.adjacency_matrix(G).todense()
A = torch.tensor(A, dtype=torch.float)Creating a GCN layer
The GCN layer is defined as follows:
\({H}^{(l+1)} = \sigma \left( \mathbf{D}^{-\frac{1}{2}} {\mathbf{\hat{A}}} \mathbf{D}^{-\frac{1}{2}} \mathbf{H}^{(l)} \mathbf{W}^{(l)} \right)\)
where \(\mathbf{H}^{(l)}\) is the \(l^{th}\) layer of the GCN, \(\mathbf{A}\) is the adjacency matrix, \({\mathbf{\hat{A}}}\) is the adjacency matrix with self-connections added, \(\mathbf{D}\) is the degree matrix, and \(\mathbf{W}^{(l)}\) is the weight matrix for the \(l^{th}\) layer.
class GCN_Layer(nn.Module):
def __init__(self, in_features, out_features):
super(GCN_Layer, self).__init__()
self.linear = nn.Linear(in_features=in_features, out_features=out_features)
def gcn_layer(self, A, D):
A_hat1 = A + torch.eye(A.shape[0], device=A.device)
return torch.matmul(torch.matmul(D, A_hat1), D)
def forward(self, A, X):
D = torch.diag(torch.sum(A+torch.eye(A.shape[0], device=A.device), dim=0) ** (-0.5))
A_hat = self.gcn_layer(A, D)
return F.relu(torch.matmul(A_hat, self.linear(X)))Creating the model
The model consists of two GCN layers and a linear layer for the output. We have used ReLU as the activation function.
class GNNModel(nn.Module):
def __init__(self, in_features, out_features, classes):
super(GNNModel, self).__init__()
self.layer1 = GCN_Layer(in_features, out_features)
self.layer2 = GCN_Layer(out_features, out_features)
self.linear = nn.Linear(out_features, classes)
def forward(self, A, X):
H = self.layer1(A, X)
H = nn.ReLU()(H)
H = self.layer2(A, H)
H = nn.ReLU()(H)
H = self.linear(H)
return nn.Softmax(dim=1)(H)Training the model
X = dataset[0].x
y = dataset[0].y
in_features = X.shape[1] # Number of input features
hidden_dim = 64 # Number of hidden features
classes = 7 # Number of classes
gcn_layer = GNNModel(in_features, hidden_dim, classes)
criterion = nn.CrossEntropyLoss() # Use cross-entropy loss for classification
optimizer = torch.optim.Adam(gcn_layer.parameters(), lr=0.01)
num_epochs = 100
for epoch in range(num_epochs):
# Forward pass
output = gcn_layer(A, X)
# Compute the loss
loss = criterion(output, y) # Assume y contains the ground truth class labels
# Backward and optimize
optimizer.zero_grad()
loss.backward()
optimizer.step()
# Compute the accuracy
predicted_labels = output.argmax(dim=1)
accuracy = (predicted_labels == y).float().mean()
# Print the loss and accuracy for monitoring
if (epoch + 1) % 1 == 0:
print(f'Epoch [{epoch+1}/{num_epochs}], Loss: {loss.item():.4f}, Accuracy: {accuracy.item():.4f}')Epoch [1/100], Loss: 1.9459, Accuracy: 0.0702
Epoch [2/100], Loss: 1.9383, Accuracy: 0.3316
Epoch [3/100], Loss: 1.9238, Accuracy: 0.3024
Epoch [4/100], Loss: 1.8966, Accuracy: 0.3021
Epoch [5/100], Loss: 1.8567, Accuracy: 0.3021
Epoch [6/100], Loss: 1.8174, Accuracy: 0.3021
Epoch [7/100], Loss: 1.7879, Accuracy: 0.3024
Epoch [8/100], Loss: 1.7328, Accuracy: 0.4346
Epoch [9/100], Loss: 1.6781, Accuracy: 0.5835
Epoch [10/100], Loss: 1.6422, Accuracy: 0.5735
Epoch [11/100], Loss: 1.5881, Accuracy: 0.6141
Epoch [12/100], Loss: 1.5457, Accuracy: 0.6647
Epoch [13/100], Loss: 1.5212, Accuracy: 0.6747
Epoch [14/100], Loss: 1.5006, Accuracy: 0.6765
Epoch [15/100], Loss: 1.4805, Accuracy: 0.6839
Epoch [16/100], Loss: 1.4607, Accuracy: 0.6994
Epoch [17/100], Loss: 1.4392, Accuracy: 0.7448
Epoch [18/100], Loss: 1.4178, Accuracy: 0.7744
Epoch [19/100], Loss: 1.4071, Accuracy: 0.7740
Epoch [20/100], Loss: 1.4041, Accuracy: 0.7707
Epoch [21/100], Loss: 1.3950, Accuracy: 0.7758
Epoch [22/100], Loss: 1.3820, Accuracy: 0.7855
Epoch [23/100], Loss: 1.3722, Accuracy: 0.7954
Epoch [24/100], Loss: 1.3673, Accuracy: 0.7939
Epoch [25/100], Loss: 1.3631, Accuracy: 0.7984
Epoch [26/100], Loss: 1.3546, Accuracy: 0.8102
Epoch [27/100], Loss: 1.3429, Accuracy: 0.8312
Epoch [28/100], Loss: 1.3326, Accuracy: 0.8475
Epoch [29/100], Loss: 1.3278, Accuracy: 0.8471
Epoch [30/100], Loss: 1.3254, Accuracy: 0.8504
Epoch [31/100], Loss: 1.3180, Accuracy: 0.8512
Epoch [32/100], Loss: 1.3070, Accuracy: 0.8634
Epoch [33/100], Loss: 1.2922, Accuracy: 0.8911
Epoch [34/100], Loss: 1.2784, Accuracy: 0.9044
Epoch [35/100], Loss: 1.2733, Accuracy: 0.9114
Epoch [36/100], Loss: 1.2694, Accuracy: 0.9114
Epoch [37/100], Loss: 1.2593, Accuracy: 0.9202
Epoch [38/100], Loss: 1.2501, Accuracy: 0.9258
Epoch [39/100], Loss: 1.2448, Accuracy: 0.9302
Epoch [40/100], Loss: 1.2408, Accuracy: 0.9321
Epoch [41/100], Loss: 1.2374, Accuracy: 0.9346
Epoch [42/100], Loss: 1.2349, Accuracy: 0.9361
Epoch [43/100], Loss: 1.2327, Accuracy: 0.9369
Epoch [44/100], Loss: 1.2304, Accuracy: 0.9394
Epoch [45/100], Loss: 1.2284, Accuracy: 0.9417
Epoch [46/100], Loss: 1.2271, Accuracy: 0.9428
Epoch [47/100], Loss: 1.2264, Accuracy: 0.9424
Epoch [48/100], Loss: 1.2256, Accuracy: 0.9428
Epoch [49/100], Loss: 1.2243, Accuracy: 0.9435
Epoch [50/100], Loss: 1.2225, Accuracy: 0.9457
Epoch [51/100], Loss: 1.2208, Accuracy: 0.9472
Epoch [52/100], Loss: 1.2198, Accuracy: 0.9490
Epoch [53/100], Loss: 1.2187, Accuracy: 0.9501
Epoch [54/100], Loss: 1.2178, Accuracy: 0.9509
Epoch [55/100], Loss: 1.2170, Accuracy: 0.9520
Epoch [56/100], Loss: 1.2161, Accuracy: 0.9531
Epoch [57/100], Loss: 1.2150, Accuracy: 0.9549
Epoch [58/100], Loss: 1.2143, Accuracy: 0.9549
Epoch [59/100], Loss: 1.2135, Accuracy: 0.9553
Epoch [60/100], Loss: 1.2129, Accuracy: 0.9564
Epoch [61/100], Loss: 1.2123, Accuracy: 0.9572
Epoch [62/100], Loss: 1.2116, Accuracy: 0.9572
Epoch [63/100], Loss: 1.2110, Accuracy: 0.9575
Epoch [64/100], Loss: 1.2104, Accuracy: 0.9579
Epoch [65/100], Loss: 1.2096, Accuracy: 0.9586
Epoch [66/100], Loss: 1.2092, Accuracy: 0.9594
Epoch [67/100], Loss: 1.2087, Accuracy: 0.9594
Epoch [68/100], Loss: 1.2083, Accuracy: 0.9594
Epoch [69/100], Loss: 1.2079, Accuracy: 0.9601
Epoch [70/100], Loss: 1.2076, Accuracy: 0.9597
Epoch [71/100], Loss: 1.2073, Accuracy: 0.9601
Epoch [72/100], Loss: 1.2070, Accuracy: 0.9601
Epoch [73/100], Loss: 1.2067, Accuracy: 0.9605
Epoch [74/100], Loss: 1.2065, Accuracy: 0.9605
Epoch [75/100], Loss: 1.2063, Accuracy: 0.9609
Epoch [76/100], Loss: 1.2061, Accuracy: 0.9612
Epoch [77/100], Loss: 1.2060, Accuracy: 0.9612
Epoch [78/100], Loss: 1.2058, Accuracy: 0.9612
Epoch [79/100], Loss: 1.2057, Accuracy: 0.9612
Epoch [80/100], Loss: 1.2054, Accuracy: 0.9616
Epoch [81/100], Loss: 1.2053, Accuracy: 0.9616
Epoch [82/100], Loss: 1.2051, Accuracy: 0.9616
Epoch [83/100], Loss: 1.2050, Accuracy: 0.9616
Epoch [84/100], Loss: 1.2050, Accuracy: 0.9616
Epoch [85/100], Loss: 1.2049, Accuracy: 0.9616
Epoch [86/100], Loss: 1.2049, Accuracy: 0.9616
Epoch [87/100], Loss: 1.2048, Accuracy: 0.9616
Epoch [88/100], Loss: 1.2047, Accuracy: 0.9616
Epoch [89/100], Loss: 1.2046, Accuracy: 0.9616
Epoch [90/100], Loss: 1.2044, Accuracy: 0.9616
Epoch [91/100], Loss: 1.2042, Accuracy: 0.9623
Epoch [92/100], Loss: 1.2041, Accuracy: 0.9620
Epoch [93/100], Loss: 1.2041, Accuracy: 0.9620
Epoch [94/100], Loss: 1.2040, Accuracy: 0.9620
Epoch [95/100], Loss: 1.2039, Accuracy: 0.9623
Epoch [96/100], Loss: 1.2038, Accuracy: 0.9627
Epoch [97/100], Loss: 1.2037, Accuracy: 0.9627
Epoch [98/100], Loss: 1.2036, Accuracy: 0.9627
Epoch [99/100], Loss: 1.2036, Accuracy: 0.9627
Epoch [100/100], Loss: 1.2036, Accuracy: 0.9627output = gcn_layer(A, X)
y_pred = output.argmax(dim=1)
y = dataset[0].y
print(f'Accuracy of GCN model: {float(((y == y_pred).sum()) / len(y))*100}')Accuracy of GCN model: 96.27031087875366